White paper
This white paper describes the Safe Notes encryption and decryption. Unless otherwise specified then is displayed schematic for the unlimited version of the safenotes subkeys.
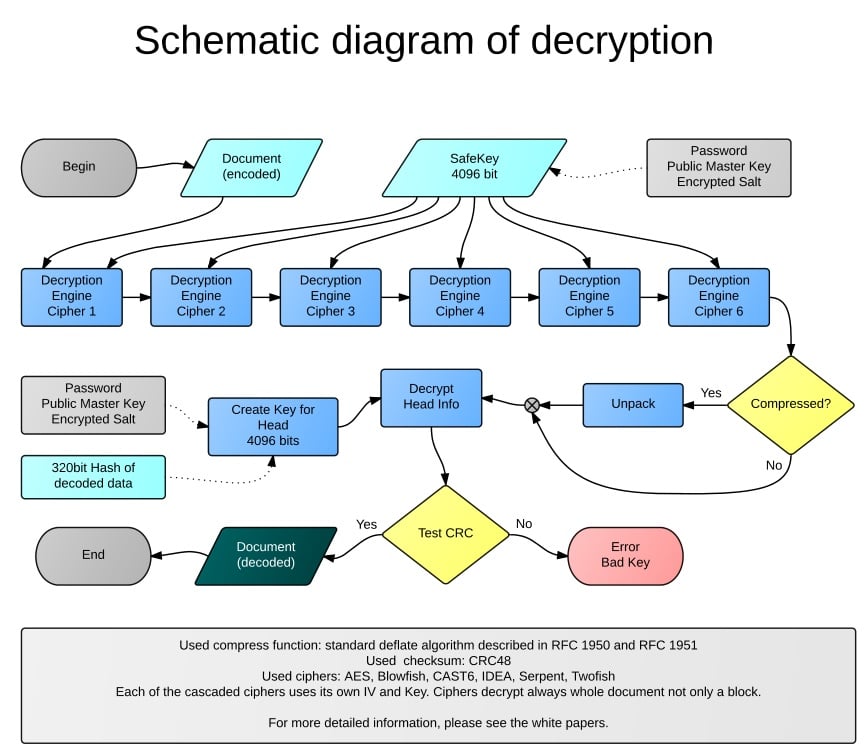
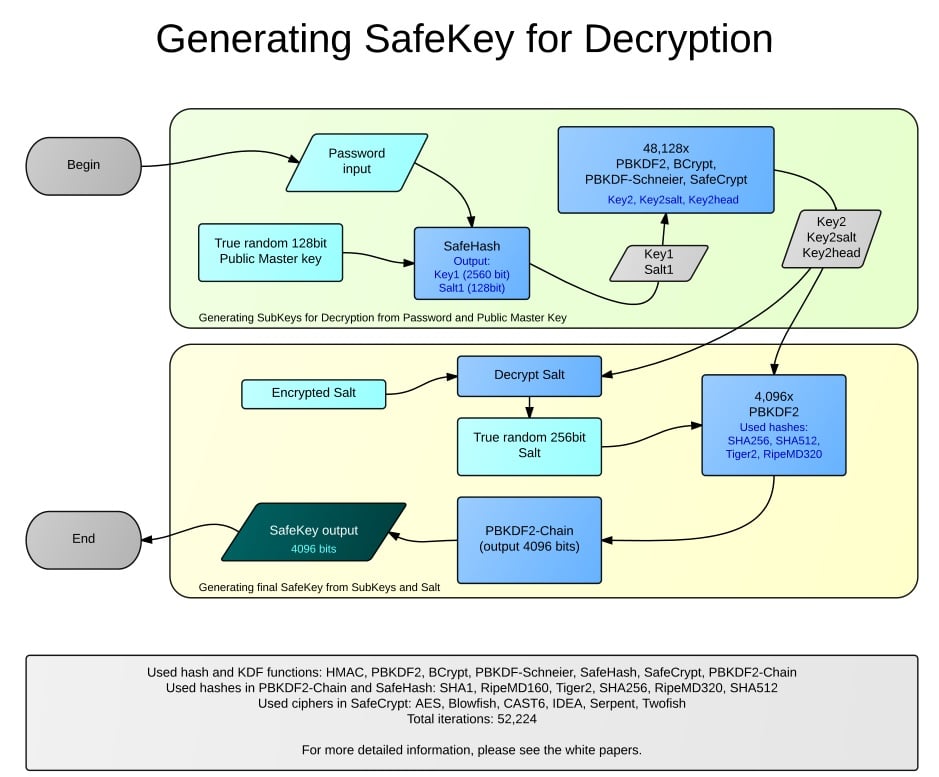
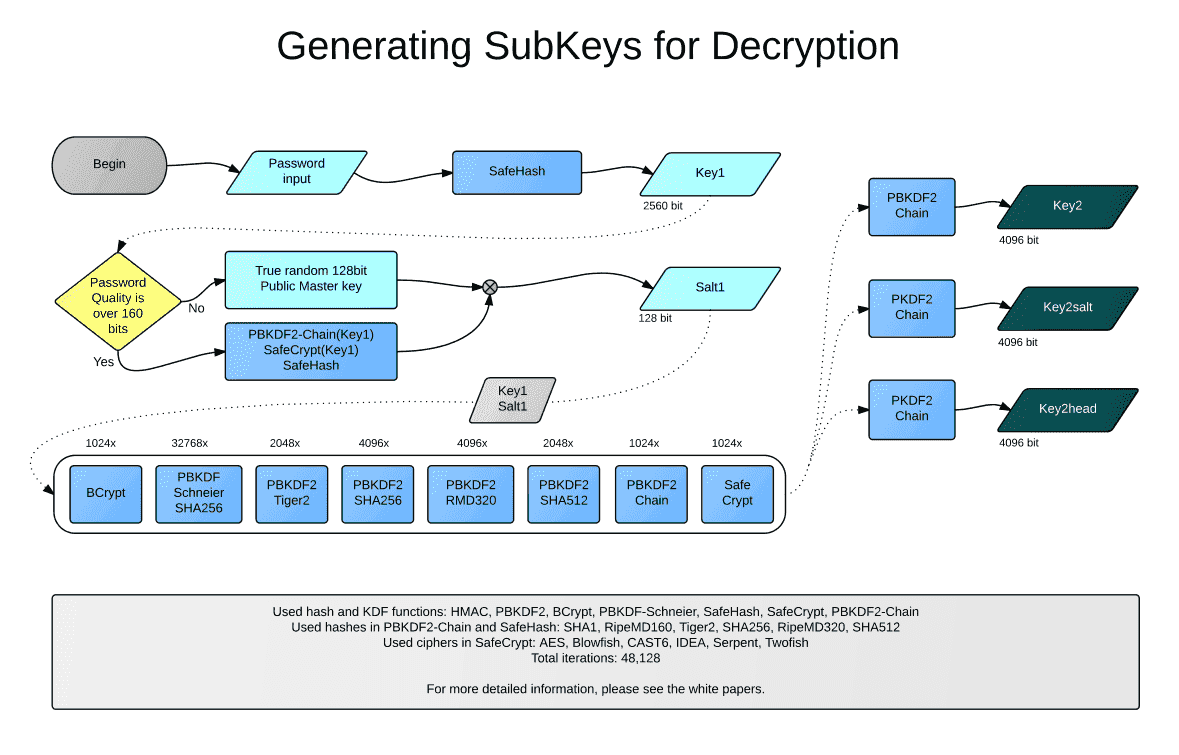
 SafeKey and its Subkeys (version 3.0)
SafeKey and its Subkeys (version 3.0)
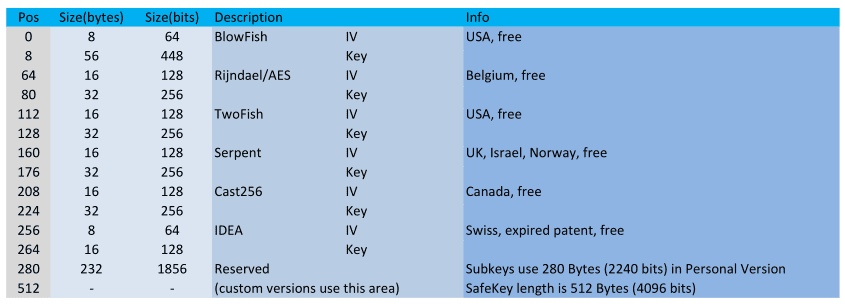 Safe Notes File Format Specification (version 3.0)
Safe Notes File Format Specification (version 3.0)
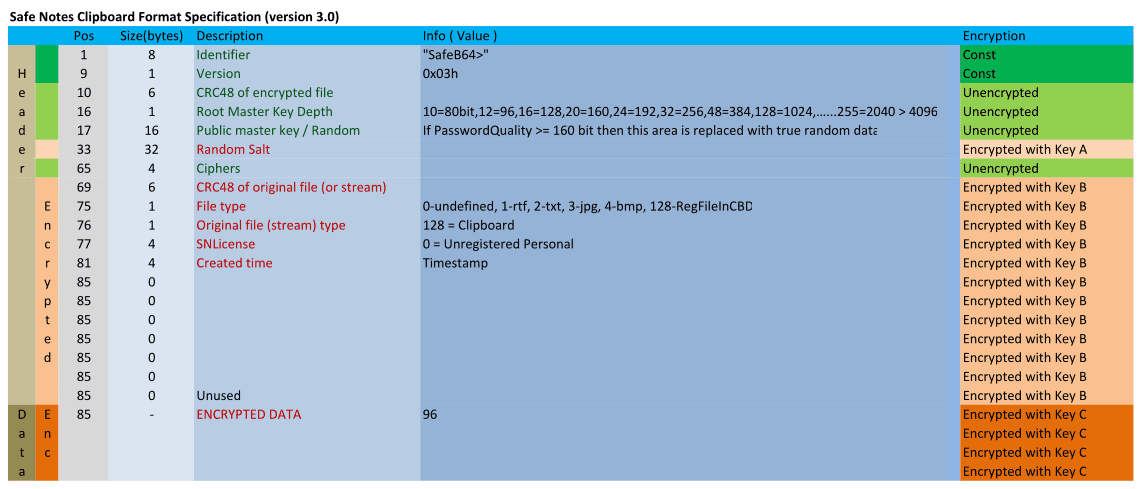
 Safe Notes Clipboard Format Specification (version 3.0)
Safe Notes Clipboard Format Specification (version 3.0)
# Description of all algorithms
Used Pascal style pseudocode in description of algorithms.
PBKDF and ciphers:BCrypt, PBKDF2 and PBKDF-Schneier are as standard defined functions with these names. AES, Blowfish, CAST6, IDEA, Serpent, Twofish are as standard defined ciphers with these names, used with maximum security settings. SHA1, SHA256, SHA512, RipeMD160, RipeMD320, Tiger(used Tiger2) are as standard defined hash functions with these names.
PBKDF2-Chain, PBKDF2x, SafeReduceLength:function PBKDF2_Chain(InHash,Salt:AnsiString; Iteration, Repeating, Out_Len:integer):AnsiString;
var
Hx,H1,H2,H3,H4,H5,H6: AnsiString; i,j: Integer;
begin
SetLength(Hx, Out_Len); fillchar(Hx[1], Out_Len, #0); if Repeating < 1 then Repeating:=1;
for j:=1 to Repeating do
begin
H1:=PBKDF2x(TFC_sha1, InHash, Salt, Iteration, Out_Len);
H2:=PBKDF2x(TFC_ripemd160, InHash+H1, Salt, Iteration, Out_Len);
H3:=PBKDF2x(TFC_Tiger, InHash+H1+H2, Salt, Iteration, Out_Len);
H4:=PBKDF2x(TFC_sha256, InHash+H1+H2+H3, Salt, Iteration, Out_Len);
H5:=PBKDF2x(TFC_ripemd320, InHash+H1+H2+H3+H4, Salt, Iteration, Out_Len);
H6:=PBKDF2x(TFC_sha512, InHash+H1+H2+H3+H4+H5, Salt, Iteration, Out_Len);
for i := 1 to Out_Len do
Hx[i] := chr(ord(Hx[i]) xor ord(H1[i]) xor ord(H2[i]) xor ord(H3[i]) xor ord(H4[i]) xor ord(H5[i]) xor ord(H6[i]));
Salt:=Hx;
end;
Result:=Hx;
end;
function PBKDF2x(HashType: TFC_Hashclass; Password, Salt: AnsiString; const C: Integer; const dkLen: Integer): AnsiString;
// for correction weak point of original PBKDF2
var blocksize: word;
begin
blocksize:=HashType.GetBlockSize; // 64 or 128 bytes
if length(Password)>blocksize then Password:=SafeReduceLength(Password, blocksize);
PBKDF2x:=PBKDF2(HashType, Password, Salt, C, dkLen);
end;
function SafeReduceLength(InStr:AnsiString;OutLen:integer):AnsiString;
var i,k: longint;
begin
k:=0;
for i:=OutLen+1 to Length(InStr) do
begin
inc(k); if k>OutLen then k:=1;
InStr[k]:=char(byte(InStr[k]) xor byte(InStr[i]));
end;
Result:=copy(InStr,1,OutLen);
end;
function SafeCrypt(InKey: AnsiString; Iteration, OutLen:integer): AnsiString;
const KeyLength=512;
var i,PKx:longint; Kx,ActKey,ActOut,Salt:AnsiString;
begin
Salt:=SafeHash(InKey);
ActOut:= PBKDF2_Chain(InKey, Salt, 2,3, KeyLength+OutLen);
ActKey:= PBKDF2_Chain(Salt+InKey, ActOut, 2,3, KeyLength);
PKx:=OutLen+1;
if Iteration>1 then Iteration:=Iteration div 2 else Iteration:=1;
for i:=1 to Iteration do
begin
Kx:=copy(ActOut,PKx,KeyLength);
EncryptString({text, key512} ActKey, Kx ); // Out 512 bytes -> key
DecryptString({text, key512} ActOut, ActKey ) // Out 512+OutLen bytes -> text
// Encryption with cascade: Blowfish-AES-Twofish-Serpent-CAST6-IDEA
end;
Result:=SafeReduceLength(ActOut, OutLen);
end;
procedure EncryptString(var Text:AnsiString; SKeys:AnsiString);
begin // Every procedure use different sections of the SKeys (4096-bit) as IV and Key
if length(SKeys)<>512 then SKeys:=PBKDF2_Chain(SKeys,SKeys, 2,3, 512);
Encrypt_BlowFish(Text, SKeys);
Encrypt_AES(Text, SKeys);
Encrypt_TwoFish(Text, SKeys);
Encrypt_Serpent(Text, SKeys);
Encrypt_Cast6(Text, SKeys);
Encrypt_Idea(Text, SKeys);
end;
procedure DecryptString(var Text:AnsiString; SKeys:AnsiString);
begin // Every procedure use different sections of the SKeys (4096-bit) as IV and Key
if length(SKeys)<>512 then SKeys:=PBKDF2_Chain(SKeys,SKeys, 2,3, 512);
Decrypt_Idea(Text, SKeys);
Decrypt_Cast6(Text, SKeys);
Decrypt_Serpent(Text, SKeys);
Decrypt_TwoFish(Text, SKeys);
Decrypt_AES(Text, SKeys);
Decrypt_BlowFish(Text, SKeys);
end;
// According to the type of license change length of subkeys
procedure SetKeys(key_length: integer; var KEY2, KEY2Salt: AnsiString);
begin
if key_length>=1024 then exit; // 1024 bit or more => unchanged
KEY2:=SafeReduceLength(KEY2, key_length div 8);
KEY2Salt:=PBKDF2_Chain(KEY2, '', 2, 3, 512);
end;
function SafeHash(const pwd: AnsiString): AnsiString;
var key:AnsiString;
begin
key:='';
Result:=GetHMAC3(key,pwd,320);
end;
function GetHMAC3(const Key, Msg:AnsiString; OutBytes:integer): AnsiString;
// replacement for HMAC (eg. HMAC-SHA512), this is much safer
var
T,H,H1,H2,H3,H4,H5,H6: AnsiString;
begin
T:=Key+Msg;
H1:=HashSHA1(T);
T:=H1+T;
H2:=HashRMD160(T);
T:=H2+T;
H3:=HashTiger(T);
T:=H3+T;
H4:=HashSHA256(T);
T:=H4+T;
H5:=HashRMD320(T);
T:=H5+T;
H6:=HashSHA512(T);
H :=H6+H5+H4+H3+H2+H1;
while length(H)<(OutBytes * 3) do
begin
H1:=HashSHA1(H);
H:=H1+H;
H2:=HashRMD160(H);
H:=H2+H;
H3:=HashTiger(H);
H:=H3+H;
H4:=HashSHA256(H);
H:=H4+H;
H5:=HashRMD320(H);
H:=H5+H;
H6:=HashSHA512(H);
H :=H6+H;
end;
Result:=SafeReduceLength(H,OutBytes);
end;
The first source is a true random pool with 16384 bits and always only the best cryptographic functions are used. The random pool changes over time according to different random input data (e.g. keyboard, mouse, apps, interruptions, CryptoAPI, HDD). The generated random data is absolutely cryptographically secure and always verifiable.
Functions for creating random data:function ComputePublicMasterKey(PMKSource: AnsiString): AnsiString;
begin
Result:=PBKDF2_Chain(PMKSource, 'PublicMasterKey', 2,3, 512);
Result:=SafeReduceLength(Result,16);
AddToEncryptedLOG(fLogPMK,PMKSource,Result); // This allows control of safety (no back-door in random data)
end;
function ComputeSalt(SaltSource: AnsiString): AnsiString;
begin
Result:=PBKDF2_Chain(SaltSource, 'Salt', 2,3, 32);
AddToEncryptedLOG(fLogSALT,SaltSource,Result); // This allows control of safety (no back-door in random data)
end;
function VerifRandom(Source: AnsiString): AnsiString;
begin
Source:=SafeReduceLength(HashSHA512(Source)+HashRMD320(Source)+HashTiger2_192(Source)+HashRMD160(Source)+HashSHA256(Source),64)+Source;
Result:=SafeReduceLength(HashSHA512(Source)+HashRMD320(Source)+HashTiger2_192(Source)+HashRMD160(Source)+HashSHA256(Source),32);
end;
function MakeSalt32VR: AnsiString;
begin
Source:=MakeSalt32; // get true random 32-byte from random pool with 16384-bits using the best cryptographic functions
Result:=VerifRandom(Source);
AddToEncryptedLOG(pmkPWD,Source,Result); // This allows control of safety (no back-door in random data)
end;
function MakeSalt32VRw: AnsiString;
begin
Source:=MakeSalt32;
Result:=VerifRandom(Source);
AddToEncryptedLOG(pmkPWD24w,Source,Result); // This allows control of safety (no back-door in random data)
end;
function GenerateRandomPassword(PwdLength:integer):AnsiString;
const
Array64='abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789??';
var
begin
P:='';
repeat
S:=MakeSalt32VR;
for i:=1 to 32 do P:=P + Array64[1+byte(S[i]) div 4]; // uses 6-bits from each byte
while pos('?',P)>0 do delete(P,pos('?',P),1); // used 62 chars; and 2 positions from 6-bit area are ignored
until length(P)>=PwdLength;
setlength(P,PwdLength);
Result:=P;
end;
function GenerateRandomPhrase24W: AnsiString;
begin
repeat
S:=MakeSalt32VRw+MakeSalt32VRw;
S:=MakeSalt32VRw+MakeSalt32VRw+S;
S:=MakeSalt32VRw+MakeSalt32VRw+S;
Words:=' '; uniq:=0;
for i:=1 to 24 do
begin
idx:=ord(s[i]);
idx:=idx*256+ord(s[i+64]); // idx = 0 .. 65535
idx:=idx*3071; // 0 .. 201389055
idx:=idx div 65535; // 0 .. 3071
w0:=GetWordFromDictionery(idx)+' '; // Dictionery with 3072 words
if pos(' '+w0,words)=0 then inc(uniq);
Words:=words+w0;
end;
delete(words,length(words),1);
delete(words,1,1);
until (length(Words)<=250)and(uniq>=22); // Size must be <251 and with 22 or more unique words
Result:=Words;
end;
function RandomSourceToPrivatKey(S: AnsiString): AnsiString;
begin
S:=SafeReduceLength(HashSHA512(S)+HashRMD320(S)+HashTiger(S)+HashRMD160(S)+HashSHA256(S),64)+S; // S is a random Source: 512-bit binary data or 24 words
if UltraSafeFlag then Password:=S[47]+S[53]+S[61]+S[3]+S[7]+S[11]+S[17]+S[19]+S[29]+S[31]+S[41]+S[43]+S[2]+S[37]+S[59]+S[5]+S[23]+S[13];
Result:=SafeReduceLength(HashSHA512(S)+HashRMD320(S)+HashTiger(S)+HashRMD160(S)+HashSHA256(S),32);
if UltraSafeFlag then EncryptString(Result, Password); // Safe vs UltraSafe difference: this code; and Ultra has a stronger quality tests for randomness
end;
function PrivatKeyToBitcoinAddress(PrivateKey: AnsiString): AnsiString;
begin
PublicKey:=ECC_PrivatKeytoPublicKey(Privatkey, CurveParam); // Elliptic-curve cryptography, Bitcoin use Secp256k1 curve
Result:=PublicKeyToBTCAdr(PublicKey, CompressFlag); // Bitcoin address, compressed or uncompressed
end;
function RandomPoolToRandomSource(PoolData: AnsiString): AnsiString;
begin
repeat
RandomSeed:=GetRandomData(Randompool); // RandomSeed is a random sequence (512-bit) created from RandomPool with strong cryptography. Random Pool is remixed and increased with new random data
RandomWords:=Create24Words(RandomSeed); // 24 words from RandomSeed, lowercase with space as a separator
if UseWordsFlag then RandomSource:=RandomWords else RandomSource:=RandomSeed;
IsGood:=Test(RandomSource, UltraSafeFlag); // if UltraSafe then is used a stronger quality tests for randomness
until IsGood;
Result:= RandomSource;
end;
// Generating Verifiable Random , up to 2048-bits, if more bits are needed, repeat the procedure
procedure SeedToVR(bits:longint; var seed,vr:AnsiString); // input and output are binary and not hexadecimal!!!
var S,Sa,Sb,Sc,Sd,Sx:AnsiString;
begin
S:=Seed; // SHA512+RMD320+Tiger2_192+RMD160+SHA256 => get 1440 bits = 180Byte
Sa:=SafeReduceLength(HashSHA512(S)+HashRMD320(S)+HashTiger(S)+HashRMD160(S)+HashSHA256(S),64);
Sx:=Sa+S;
Sb:=SafeReduceLength(HashRMD320(Sx)+HashTiger(Sx)+HashSHA512(Sx)+HashSHA256(Sx)+HashRMD160(Sx),64);
Sx:=Sb+S;
Sc:=SafeReduceLength(HashSHA512(Sx)+HashRMD320(Sx)+HashTiger(Sx)+HashRMD160(Sx)+HashSHA256(Sx),64);
Sx:=Sc+S;
Sd:=SafeReduceLength(HashRMD320(Sx)+HashTiger(Sx)+HashSHA512(Sx)+HashSHA256(Sx)+HashRMD160(Sx),64);
Sx:=SafeReduceLength(Sd+Sb+Sc+Sa, bits div 8); // max 64*4=256Byte=2048bit }
VR:=Sx;
end;
// replacement for PBKDF2, this is much much more safer
// used only in customversions
# Test Vectors
Hash test vectors:Input: ""
SHA1 : ( DA 39 A3 EE 5E 6B 4B 0D 32 55 BF EF 95 60 18 90 AF D8 07 09 )
RMD160: ( 9C 11 85 A5 C5 E9 FC 54 61 28 08 97 7E E8 F5 48 B2 25 8D 31 )
Tiger2: ( 44 41 BE 75 F6 01 87 73 C2 06 C2 27 45 37 4B 92 4A A8 31 3F EF 91 9F 41 )
SHA256: ( E3 B0 C4 42 98 FC 1C 14 9A FB F4 C8 99 6F B9 24 27 AE 41 E4 64 9B 93 4C A4 95 99 1B 78 52 B8 55 )
RMD320: ( 22 D6 5D 56 61 53 6C DC 75 C1 FD F5 C6 DE 7B 41 B9 F2 73 25 EB C6 1E 85 57 17 7D 70 5A 0E C8 80 15 1C 3A 32 A0 08 99 B8 )
SHA512: ( CF 83 E1 35 7E EF B8 BD F1 54 28 50 D6 6D 80 07 D6 20 E4 05 0B 57 15 DC 83 F4 A9 21 D3 6C E9 CE 47 D0 D1 3C 5D 85 F2 B0 FF 83 18 D2 87 7E EC 2F 63 B9 31 BD 47 41 7A 81 A5 38 32 7A F9 27 DA 3E )
Input: "The quick brown fox jumps over the lazy dog"
SHA1 : ( 2F D4 E1 C6 7A 2D 28 FC ED 84 9E E1 BB 76 E7 39 1B 93 EB 12 )
RMD160: ( 37 F3 32 F6 8D B7 7B D9 D7 ED D4 96 95 71 AD 67 1C F9 DD 3B )
Tiger2: ( 97 6A BF F8 06 2A 2E 9D CE A3 A1 AC E9 66 ED 9C 19 CB 85 55 8B 49 76 D8 )
SHA256: ( D7 A8 FB B3 07 D7 80 94 69 CA 9A BC B0 08 2E 4F 8D 56 51 E4 6D 3C DB 76 2D 02 D0 BF 37 C9 E5 92 )
RMD320: ( E7 66 0E 67 54 94 35 C6 21 41 E5 1C 9A B1 DC C3 B1 EE 9F 65 C0 B3 E5 61 AE 8F 58 C5 DB A3 D2 19 97 78 1C D1 CC 6F BC 34 )
SHA512: ( 07 E5 47 D9 58 6F 6A 73 F7 3F BA C0 43 5E D7 69 51 21 8F B7 D0 C8 D7 88 A3 09 D7 85 43 6B BB 64 2E 93 A2 52 A9 54 F2 39 12 54 7D 1E 8A 3B 5E D6 E1 BF D7 09 78 21 23 3F A0 53 8F 3D B8 54 FE E6 )
Input: 1 million times "a"
SHA1 : ( 34 AA 97 3C D4 C4 DA A4 F6 1E EB 2B DB AD 27 31 65 34 01 6F )
RMD160: ( 52 78 32 43 C1 69 7B DB E1 6D 37 F9 7F 68 F0 83 25 DC 15 28 )
Tiger2: ( E0 68 28 1F 06 0F 55 16 28 CC 57 15 B9 D0 22 67 96 91 4D 45 F7 71 7C F4 )
SHA256: ( CD C7 6E 5C 99 14 FB 92 81 A1 C7 E2 84 D7 3E 67 F1 80 9A 48 A4 97 20 0E 04 6D 39 CC C7 11 2C D0 )
RMD320: ( BD EE 37 F4 37 1E 20 64 6B 8B 0D 86 2D DA 16 29 2A E3 6F 40 96 5E 8C 85 09 E6 3D 1D BD DE CC 50 3E 2B 63 EB 92 45 BB 66 )
SHA512: ( E7 18 48 3D 0C E7 69 64 4E 2E 42 C7 BC 15 B4 63 8E 1F 98 B1 3B 20 44 28 56 32 A8 03 AF A9 73 EB DE 0F F2 44 87 7E A6 0A 4C B0 43 2C E5 77 C3 1B EB 00 9C 5C 2C 49 AA 2E 4E AD B2 17 AD 8C C0 9B )
Input: message="" key=""
HMAC SHA1: ( FB DB 1D 1B 18 AA 6C 08 32 4B 7D 64 B7 1F B7 63 70 69 0E 1D )
HMAC RMD160: ( 44 D8 6B 65 8A 3E 7C BC 1A 20 10 84 8B 53 E3 5C 91 77 20 CA )
HMAC Tiger2: ( 19 73 0A A3 A7 F4 D1 15 2A B3 39 7C 33 46 CC 19 5E CC 42 A4 A6 0B 53 FD )
HMAC SHA256: ( B6 13 67 9A 08 14 D9 EC 77 2F 95 D7 78 C3 5F C5 FF 16 97 C4 93 71 56 53 C6 C7 12 14 42 92 C5 AD )
HMAC RMD320: ( 9E 16 B9 9B AB B1 D4 9E E2 E6 21 F1 E7 71 89 25 12 FF 3C 24 64 F7 40 11 9D E0 3D DC 9A 56 3A A4 73 E7 5B C2 68 29 AE EE )
HMAC SHA512: ( B9 36 CE E8 6C 9F 87 AA 5D 3C 6F 2E 84 CB 5A 42 39 A5 FE 50 48 0A 6E C6 6B 70 AB 5B 1F 4A C6 73 0C 6C 51 54 21 B3 27 EC 1D 69 40 2E 53 DF B4 9A D7 38 1E B0 67 B3 38 FD 7B 0C B2 22 47 22 5D 47 )
Input: message="what do ya want for nothing?" key="Jefe"
HMAC SHA1: ( EF FC DF 6A E5 EB 2F A2 D2 74 16 D5 F1 84 DF 9C 25 9A 7C 79 )
HMAC RMD160: ( DD A6 C0 21 3A 48 5A 9E 24 F4 74 20 64 A7 F0 33 B4 3C 40 69 )
HMAC Tiger2: ( 6E BE 22 54 70 66 51 95 D7 E7 0D 77 DC 21 83 2C 41 2B 78 22 27 4B D4 C0 )
HMAC SHA256: ( 5B DC C1 46 BF 60 75 4E 6A 04 24 26 08 95 75 C7 5A 00 3F 08 9D 27 39 83 9D EC 58 B9 64 EC 38 43 )
HMAC RMD320: ( E4 40 B0 0B 63 26 E4 F7 DA D3 A6 59 1E 81 89 E9 70 8F C1 7E 3C AB 30 6F C6 7E FA F7 09 47 AA D2 EA 89 E2 8F 79 D0 3B D3 )
HMAC SHA512: ( 16 4B 7A 7B FC F8 19 E2 E3 95 FB E7 3B 56 E0 A3 87 BD 64 22 2E 83 1F D6 10 27 0C D7 EA 25 05 54 97 58 BF 75 C0 5A 99 4A 6D 03 4F 65 F8 F0 E6 FD CA EA B1 A3 4D 4A 6B 4B 63 6E 07 0A 38 BC E7 37 )
Input: password="password" salt="salt" iterations=4096 dkLen=20
PBKDF2 SHA1: ( 4b 00 79 01 b7 65 48 9a be ad 49 d9 26 f7 21 d0 65 a4 29 c1 )
Input: password="password" salt="salt" iterations=16777216 dkLen=20
PBKDF2 SHA1: ( ee fe 3d 61 cd 4d a4 e4 e9 94 5b 3d 6b a2 15 8c 26 34 e9 84 )
Input: password="passwordPASSWORDpassword" salt="saltSALTsaltSALTsaltSALTsaltSALTsalt" iterations=4096 dkLen=25
PBKDF2 SHA1: ( 3d 2e ec 4f e4 1c 84 9b 80 c8 d8 36 62 c0 e4 4a 8b 29 1a 96 4c f2 f0 70 38 )
Input: password="pass\0word" salt="sa\0lt" iterations=4096 dkLen=16
PBKDF2 SHA1: ( 56 fa 6a a7 55 48 09 9d cc 37 d7 f0 34 25 e0 c3 )
Input: password="pa\0ss" salt="sa\0lt" iterations=320 dkLen=28
PBKDF2-SHA1: ( 2F 77 FE AB 3D 33 0E 50 03 C0 38 05 60 74 98 21 35 26 CD D9 27 A1 A6 5D 89 5F 5C C1 )
PBKDF2-RMD160: ( A8 7B 54 3C 08 74 91 D5 62 A5 5F B6 4C 80 38 0B 82 22 92 C6 E2 AB 38 3D 25 1C F3 3E )
Input: password="pa\0ss" salt="sa\0lt" iterations=320 dkLen=32
PBKDF2-Tiger2: ( B3 50 BE 8C 13 D4 1C 65 47 5F F6 AA 25 FD DB EA D7 13 7E 24 39 2B 4F 83 AB ED C5 74 6B DE 4F 24 )
Input: password="pa\0ss" salt="sa\0lt" iterations=320 dkLen=40
PBKDF2-SHA256: ( B9 D2 72 2D 7E 0E 48 5C FD 89 A6 7A CE 9C 60 9C D7 7D C8 D7 EE ED 27 5B 1B E3 FB BF EF AF 33 19 6D EF CE 54 86 C3 2C 6B )
Input: password="pa\0ss" salt="sa\0lt" iterations=320 dkLen=48
PBKDF2-RMD320: ( 4D C1 7C 66 8E 79 C9 29 23 E6 AD 02 CC 89 14 95 D9 AE 4D 27 8D AF 59 5D 21 E3 D0 2A 40 12 2D F3 DC 4B 97 A4 48 89 CE 7D C3 0C 74 EC CE 30 44 F6 )
Input: password="pa\0ss" salt="sa\0lt" iterations=320 dkLen=72
PBKDF2-SHA512: ( 00 EC 72 AC 46 7F AF EF 7D A3 68 68 FA 38 2A 1D 47 65 7D F6 51 48 7F 72 4C 01 E9 6F 9C 55 60 31 81 BA 96 4D 6E A0 A5 56 C6 80 E6 0C 41 14 68 1C 36 61 2A DB 9A 0D 5E 9C 98 9F 9A 0E A2 07 D1 0A 15 2C 16 EA 61 5C A4 E3 )
Input: password="pa\0ss" salt="sa\0lt" iterations=7 repeating=5 OutLen=72
PBKDF2-Chain: ( E3 31 04 A3 7F 00 97 ED A1 C7 30 EF B2 2D 5D 0A 51 89 F7 CD 97 5B 0A A0 CA FA 2A D5 17 D7 A9 76 D5 B7 4A B4 2A D4 AF 29 5D 92 D0 59 D6 FF 10 92 C4 4E 89 60 D3 DD D8 90 1D F8 A2 F2 1F F3 D8 8C 38 24 86 6E AF 70 0B 9D )
Input: password="pa\0ss" salt="sa\0lt" iterations=7 repeating=5 OutLen=73
PBKDF2-Chain: ( D4 E5 1E 6C 03 90 B3 24 B5 85 40 96 12 22 5F 83 C1 2E 73 51 F1 70 E8 29 79 75 A9 6E CB A9 44 88 EF 4B 66 F4 25 84 A9 D2 1E FE 87 15 F1 3B 38 BB 89 90 DA 56 47 1F 9A C1 00 80 01 6F 6E 5B F0 BE EE FC 4C DC BA 9E 03 AE 37 )
Input: inkey="pa\0sssa\0lt" iterations=256 OutLen=32
SafeCrypt: ( 24 18 A3 35 0B C2 11 7B F2 FE 95 43 E3 94 40 77 3B 87 2C 80 60 AD EF E6 37 6E 5B F2 9A 23 51 04 )
Input: inkey="pa\0sssa\0lt" iterations=256 OutLen=33
SafeCrypt: ( C1 DA 8D 50 19 B5 9D 96 F0 56 A0 D2 B9 F9 E1 4B 24 E7 20 0B 11 DC CA 52 94 CE 0E 24 EB 7A 08 35 C3 )
Input: inkey="pa\0sssa\0lt"
SafeHash: ( 76 3D 7A 8B 11 47 20 69 55 85 93 60 59 83 40 E6 10 2C CB 92 C5 5F 46 53 8E 66 CF 4B 9C 16 82 7B ED 73 2E B1 91 EE 97 E9 0D 68 10 4E 66 E1 81 09 8F F1 73 A1 BE 5E 09 81 17 8A 18 E8 C2 86 EB 7A 26 6C 4B E5 AC B9 B3 C3 07 9C E3 9D 46 75 B8 CF 78 FF 68 B3 30 DE 59 4F 84 42 F7 79 61 86 56 07 88 3A 08 50 C1 C3 9D 16 D3 A9 14 37 44 B8 2D 0B F5 27 C2 BB 22 63 3D 86 7B FA 60 82 79 FC 7E 02 BB E2 E3 9B C2 50 6B B8 D8 AB D4 75 99 0C AD F7 38 15 EE 5D 96 CF 5D BC 5D 43 8C D5 BA 06 AF 3F 46 CF 98 85 CC 40 23 74 9D 51 1C 08 FB 9E 97 E0 1C AD A6 ED 75 65 D0 9B 90 C7 FE D9 12 B0 00 9D 7A F7 00 9D C6 B9 4E 78 45 33 62 51 8A A0 30 9E B4 9E 0F CB 8D 08 07 D2 EA 6C 65 55 1D 11 72 25 7F 63 F7 D4 A0 E4 88 6F B2 62 31 83 39 6F 1E E6 C4 E0 6C 01 B5 57 5C F1 6E 1B 34 97 5C AA 87 )
Input: inkey="pa\0sssa\0lt\0"
SafeHash: ( 75 BE 04 DF E4 EC E2 75 7B A4 04 9C 49 6A F4 D9 FB D8 89 5C 6A B3 10 D9 0F 7B 48 AC 69 52 4D 5F 36 3F 04 36 C5 DE 23 A1 BF BC BB 6E 93 5B 1A DD CF 8C 0B D8 BA B3 56 AD 15 67 FA E5 49 3C 31 72 54 4B 8D 4E 54 68 17 8B 54 E3 5E 9C 56 D5 B8 1A B3 21 44 18 F0 01 20 0C C0 E1 02 AE 44 AD 78 97 B1 71 AD A9 84 26 8E E8 E4 D7 F9 04 AC FA A5 C9 F1 2F 3F CF 74 45 CF 65 1D A8 CD C2 B7 D1 05 1A EE F3 52 E9 6E 9B C4 6A 87 CD 0A 17 90 CE E9 D1 6B 8C 97 5E A3 83 CB FC 36 16 52 09 61 46 A7 D7 D6 74 E1 27 A1 5A C8 E5 8A 16 8F 6C B9 10 44 3A 8C 52 3B B7 25 23 C6 FB 95 77 A5 72 2A 18 8E 08 30 BC 3F 4B 7D 2E E0 60 B1 A7 CA 50 BC 16 E3 83 EE 31 9A 8B CC 95 A6 BA D2 92 40 30 5A 5A 3B FE 01 13 6D 5D 69 E3 BC 48 B6 D9 49 2D F7 21 2C BC 60 22 8C FF A8 FA 1D FA 3C AF C9 70 8C 4D 09 )